Inheritance diagram for shapes3d.path.BCurve3D:

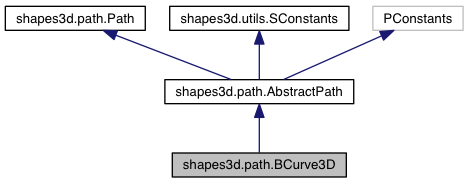
Public Member Functions
	BCurve3D (float[][] points, int nbrSlices)

	BCurve3D (float[][] points, int nbrSlices, PathOrthogonal ortho)

	BCurve3D (List< PVector > points, int nbrSlices)

	BCurve3D (List< PVector > points, int nbrSlices, PathOrthogonal ortho)

	BCurve3D (PVector[] points, int nbrSlices)

	BCurve3D (PVector[] points, int nbrSlices, PathOrthogonal ortho)

PVector	point (float t)

PVector	tangent (float t)

float	length (float t0, float t1, int steps)

float	length (int steps)

Public Member Functions inherited from shapes3d.path.AbstractPath
int	nbrSlices ()

PVector	tangent (float t)

PVector	orthogonal (float t)

boolean	isOpenPath ()

Additional Inherited Members
Public Attributes inherited from shapes3d.path.AbstractPath
PathOrthogonal	orthoCalculator = null

Public Attributes inherited from shapes3d.utils.SConstants
int	WIRE = 0x00000011

int	SOLID = 0x00000012

int	TEXTURE = 0x00000014

int	DRAWALL = WIRE \| SOLID \| TEXTURE

int	WHITE = 0xFFFFFFFF

int	BLACK = 0xFF000000

int	GREY = 0xFFC0C0C0

int	RED = 0xFFFF0000

int	GREEN = 0xFF00FF00

int	BLUE = 0xFF0000FF

int	YELLOW = 0xFFFFFF00

int	PURPLE = 0xFFFF00FF

int	CYAN = 0xFF00FFFF

int	ORANGE = 0xFFFFC000

int	CW = 1

int	CCW = 2

int	ALL = 0b11111111

int	BOTTOM = 0b00000001

int	TOP = 0b00000010

int	FRONT = 0b00000100

int	BACK = 0b00001000

int	LEFT = 0b00010000

int	RIGHT = 0b00100000

int	BODY = 0b00000001

int	END0 = 0b00000010

int	END1 = 0b00000100

float	ONE_DEG_T = (float) (Math.PI / 180.0)

PathOrthogonal	ORTHO_X = new PathOrthogonal.PathNormalX()

PathOrthogonal	ORTHO_Y = new PathOrthogonal.PathNormalY()

PathOrthogonal	ORTHO_Z = new PathOrthogonal.PathNormalZ()

PathOrthogonal	ORTHO_A = new PathOrthogonal.PathNormalAMC()

TransformUV	ROT_0 = TransformUV.ROT0

TransformUV	ROT_90 = TransformUV.ROT90

TransformUV	ROT_180 = TransformUV.ROT180

TransformUV	ROT_270 = TransformUV.ROT270

TransformUV	FLIP_H = TransformUV.FLIPH

TransformUV	FLIP_V = TransformUV.FLIPV

Rotation	ROTATION_ZERO = new Rotation()

int	T_BOX = 0x1001

int	T_DOME = 0x1002

int	T_CONE = 0x1003

int	T_ELLIPSOID = 0x1004

int	T_EXTRUSION = 0x1005

int	T_LATHESTOCK = 0x1006

int	T_MD2 = 0x1007

int	T_SKYBOX = 0x1008

int	T_SKYDOME = 0x1009

int	T_TERRAIN = 0x100A

int	T_TUBE = 0x100B

int	C_LATHESURFACE = 0x2001

int	C_OVAL = 0x2002

int	C_POLYGON = 0x2003

int	P_BCURVE2D = 0x3001

int	P_BCURVE3D = 0x3002

int	P_BSPLINE2D = 0x3003

int	P_BSPLINE3D = 0x3004

int	P_LINEAR = 0x3005

int	P_LISSAJOUS = 0x3006

int	P_RING = 0x3007

int	P_SPIRAL = 0x3008

Protected Member Functions inherited from shapes3d.path.AbstractPath
	AbstractPath ()

	AbstractPath (int nbrSlices)

Protected Attributes inherited from shapes3d.path.AbstractPath
final int	DEFAULT_NBR_SLICES = 100

final int	nbrSlices

boolean	pathIsOpen = true

Detailed Description

This class is used to represent a single Bezier curve of degree ≥ 2 in 3D space.
Note the degree of a Bezier curve equals the number of control points.
Its primary purpose is to act as a convenience class to maintain a collection Bezier controls points in 3 dimensions.

In this library the P_Bezier3D object is used by the BezTube class to create a tube that bends along by rotating it about the Y axis [0,1,0].

Degree  Shape                   


  2     straight line           


  3     quadratic bezier        


  4     cubic bezier            


  and so on

It can also be used as a path for an Extrusion.

Based on source code found on the Internet and modified by the author to work directly with Processing. The URL for the original code has been lost).

Author: Peter Lager

Constructor & Destructor Documentation

shapes3d.path.BCurve3D.BCurve3D	(	float	points[][],
		int	nbrSlices
	)

Creates a Bezier object using an array of control point positions. The bezier curve will use all of the points in the array.

Parameters

points	2D array[point no.][x/y/z] of control point positions
nbrSlices	the number of mesh sections along the path Creates a Bezier object using an array of control point positions. The bezier curve will use all of the points in the array.
points	2D array[point no.][x/y/z] of control point positions
nbrSlices	the number of mesh sections along the path
ortho	the orthogonal calculator to use Create a Bezier curve that passes through the specified positions
points	array of PVectors defining the spline.
nbrSlices	the number of slices along the length of the path Create a Bezier curve that passes through the specified positions
points	list of PVectors defining the spline.
nbrSlices	the number of slices along the length of the path
ortho	the orthogonal calculator to use Creates a Bezier object using an array of control point positions. The bezier curve will use all of the points in the array.
points	array of vertices defining the hull for this Bezier curve
nbrSlices	the number of mesh sections along the path Creates a Bezier object using an array of control point positions. The bezier curve will use all of the points in the array.
points	array of vertices defining the hull for this Bezier curve
nbrSlices	the number of mesh sections along the path
ortho	the orthogonal calculator to use Creates a Bezier object using an array of control point positions. The bezier curve will use all of the points in the array.
points	2D array[point no.][x/y/z] of control point positions
nbrSlices	the number of mesh sections along the path

shapes3d.path.BCurve3D.BCurve3D	(	float	points[][],
		int	nbrSlices,
		PathOrthogonal	ortho
	)

Creates a Bezier object using an array of control point positions. The bezier curve will use all of the points in the array.

Parameters

points	2D array[point no.][x/y/z] of control point positions
nbrSlices	the number of mesh sections along the path
ortho	the orthogonal calculator to use

shapes3d.path.BCurve3D.BCurve3D	(	List< PVector >	points,
		int	nbrSlices
	)

Create a Bezier curve that passes through the specified positions

Parameters

points	array of PVectors defining the spline.
nbrSlices	the number of slices along the length of the path

shapes3d.path.BCurve3D.BCurve3D	(	List< PVector >	points,
		int	nbrSlices,
		PathOrthogonal	ortho
	)

Create a Bezier curve that passes through the specified positions

Parameters

points	list of PVectors defining the spline.
nbrSlices	the number of slices along the length of the path
ortho	the orthogonal calculator to use

shapes3d.path.BCurve3D.BCurve3D	(	PVector[]	points,
		int	nbrSlices
	)

Creates a Bezier object using an array of control point positions. The bezier curve will use all of the points in the array.

Parameters

points	array of vertices defining the hull for this Bezier curve
nbrSlices	the number of mesh sections along the path

shapes3d.path.BCurve3D.BCurve3D	(	PVector[]	points,
		int	nbrSlices,
		PathOrthogonal	ortho
	)

Creates a Bezier object using an array of control point positions. The bezier curve will use all of the points in the array.

Parameters

points	array of vertices defining the hull for this Bezier curve
nbrSlices	the number of mesh sections along the path
ortho	the orthogonal calculator to use

Member Function Documentation

float shapes3d.path.BCurve3D.length	(	float	t0,
		float	t1,
		int	steps
	)

Calculate the path length of a section of Bezier curve.
There is no formula for the exact length of a Bezier curve so any method will always be approximate.
This method will always 'underestimate' the actual path length. It works by subdividing the Bezier curve into a number of straight line segments and summing their lengths.
The number of subdivisions can be increased to the accuracy of the result but at the cost of additional computation.
You may want to experiment but 100+ subdivisions normally give quite good results.

Parameters

t0	start ( ≥0.0 and <t1 )
t1	end ( >t0 and ≤1.0 )
steps	number of subdivisions

Returns: length of the curve section

float shapes3d.path.BCurve3D.length ( int steps )

Calculate the path length of the Bezier curve.
There is no formula for the exact length of a Bezier curve so any method will always be approximate.
This method will always 'underestimate' the actual path length. It works by subdividing the Bezier curve into a number of straight line segments and summing their lengths.
The number of subdivisions can be increased to the accuracy of the result but at the cost of additional computation.
You may want to experiment but 100+ subdivisions normally give quite good results.

Parameters

steps number of subdivisions

Returns: length of the curve

PVector shapes3d.path.BCurve3D.point ( float t )

virtual

Calculate the point for a given parametric point 't' on the bezier curve.

Parameters

t	parametric value ≥0.0 and ≤1.0

Returns: (x,y) position for given t value

Implements shapes3d.path.AbstractPath.

PVector shapes3d.path.BCurve3D.tangent ( float t )

Calculate the tangent vector for a point on the bezier curve

Parameters

t	parametric value ≥0.0 and ≤1.0

Returns: the tangent vector (normalized)

Implements shapes3d.path.Path.

The documentation for this class was generated from the following file:

/Users/peter/git/shapes3d-repos/Shapes 3D/src/shapes3d/path/BCurve3D.java

Public Member Functions

Additional Inherited Members

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation