Navigation Meshes and Path Finding

In mathematics and computer science, there is a useful mathematical abstraction called a graph. In this library we use a graph to model a network of paths that an agent can use to navigate around the game world. In this context the graph is called a 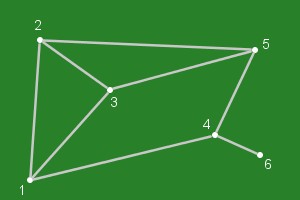graph navigation mesh.

The graph comprises of nodes (world positions an agent can visit) and edges (the connections between the nodes).

.

The picture on the right shows a simple 6-node mesh and the connections (edges) between them. It would seem that an agent could move from any node to any other node, passing along the edges in either direction without restriction.

What if we want to be enable an agent to move to node 2 from any connected node, but once at node 2 the agent can only move to node 5. In other words the connection between nodes 1 & 2 and nodes 2 & 3 are one way only. If we modify the graph image to show not just the connections but also the directions an agent to travel we get a digraph.

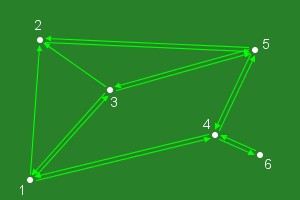digraph Looking at the picture it is possible to find paths between nodes. So for instance assume that there is an agent at node 6 and we want the agent to traverse the graph to node 2, if we stipulate that a node can only be visited once then there are just six possible paths

6 4 5 2
6 4 5 3 2
6 4 5 3 1 2
6 4 1 2
6 4 1 3 2
6 4 1 3 5 2
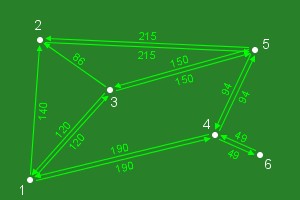
digraph with weights

but which one is best, and what do we mean by best?

If best is the ‘shortest distance to travel’ and if we know the connection distances then we could calculate the distance of each path and pick the shortest path. This picture shows the edges labelled with the connection distances, I will leave you to work out the best path.

What if we wanted the fastest path instead of the shortest distance, would the result be the same? Possibly but not necessarily it would depend on how fast we could travel along an edge. The solution would be to re-label the edges with the time it takes to traverse it instead of the distances. In this case the time it takes to travel between nodes might be different depending on which direction you are going!

In more general terms we say that there is a cost associated with traversing an edge path finding is the process of trying to find the path with the smallest cost.

Graph

The Graph class is used to represent a navigation mesh and has methods to manage the nodes and edges that make up the mesh

Nodes

The GraphNode class is used to represents nodes on the mesh. When creating a node the user must specify

  1. a unique ID number (integer)
  2. its x and y world coordinates

The ID number is used to identify a particular node in the mesh so it is important to make sure it is unique.

Edges

The GraphEdge class is used to represent a one-way connection between 2 nodes. This means that if a connection between two nodes can be traversed in both directions then 2 GraphEdge objects are required. So in the digraph above, there are in fact 14 edges!

In most cases the user does not have to work with GraphEdge objects directly, they are created by the Graph class provide the user specifies

  1. the ID number of the start node
  2. the ID number of the end node
  3. the cost of traversing from the start to end node
  4. the cost of traversing back from the end to the start node (Optional - used for bidirectional connections)

Path Finding

There is not much point to having a graph if there is no means to calculate paths between nodes. The library provides four path finding algorithms -

  1. BFS (Breadth first search)
  2. DFS (Depth first search)
  3. Dijkstra
  4. A* (pronounced A star) using 'Manhattan' or 'Crow Flight' heuristic

There many resources on the Internet that describe these algorithms in mind-boggling detail so I won't do that here. In most scenarios the A* with Crow Flight heuristic is likely to provide the best or, at least an acceptable solution.

Some examples of creating meshes and using path finding can be found in the Programming Guides.

Summary

The graph implementation in this library is both generic and flexible in that it provides a one-size fits all solution. Advanced users can add addition functionality by extending the GraphNode and GraphEdge classes to suit their needs. They can also code and use their own path-finding algorithms.